1 はじめに
近年,MIを活用したデータ駆動型の開発手法は,材料開発プロセスの革新技術として注目を集め,急速に広まりつつある。これまでの材料設計やプロセス条件の決定では,技術者の勘や経験に依存する事が多く,その検証に莫大な時間やコストを要していた。MIでは,機械学習を始めとするデータ解析技術の発達により,実験データの解析による新規材料の物性値の予測や製造方法の最適化技術等の促進が期待される。
しかし,MIの利用は大量のデータの存在が前提であり,データセット構築が課題となる。データを取得する方法は①オープンデータベースの利用,②文献からの取得,③社内の過去データの利用,④理論科学計算の利用,⑤実験による取得,に大別できる(Fig. 1)。①~③の手法は低いデータ取得コストで大規模なデータを入手しやすいが,異なる実験条件や欠損値のために有効なデータが限定される場合が多い。④においては,データ数の拡充と共に,実験では得られない情報を説明変数に組み込むことができる1)。⑤においては,人手による実験作業によってデータを得るため,データ取得コストが大きくなりやすい。そのため,大規模データセット構築には,ハイスループット実験を活用して物性データを大量に取得し,そのデータを特定フォーマットで蓄積,整形し,データベースに格納していく必要がある2)。
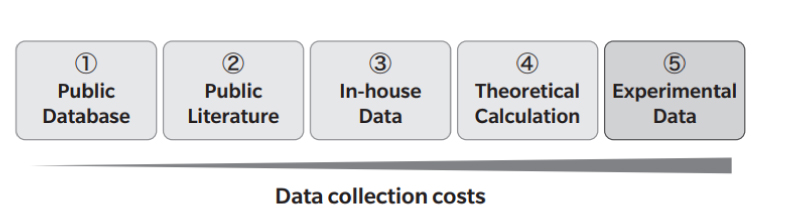
Fig. 1 Methods and costs for collecting data.
一般的にλmaxの予測には,時間依存DFT計算(以降TDDFT計算と称す)で算出した吸収波長を活用することが多いが,類似の化合物骨格間での定性的な議論に留まることが多く,その予測精度には課題が残る。TDDFT計算で算出した結果を追加の説明変数として機械学習に組み込むことで,予測精度の向上が期待できる。
ハイスループット実験は試料調整,分注,物性測定などのルーチンな実験操作を自動化・並列化することでデータを効率良く取得していく手法である。ハイスループット実験で得た膨大なデータを機械学習で解析することで,反応条件を最適化した研究も報告されている3)。
本稿では,膨大な有機化合物の候補から所望する物性を示す化合物の選定手法を開発するため,④理論科学計算,⑤ハイスループット実験によって構築したデータセットを利用し,λmaxの予測モデル作成を実施した。目的変数となるλmaxをハイスループット実験で効率的に取得するとともに,TDDFT計算で求めた吸収波長を説明変数として活用することで,機械学習によるλmaxを精度良く予測できることを実証した。本稿の第二節では,実験データを効率良く取得するためにハイスループット実験を導入した結果について述べる。第三節では,機械学習を行うために必要な説明変数の生成方法について記載する。第四節では,λmaxの予測モデルの作成と,その予測モデルの予測精度と適用範囲について考察をする。最後に,今後の展望を述べて結びとする。
2 ハイスループット実験によるデータ収集
一般に精度の良い機械学習を行う際には大量のデータを要するため,実験データを如何に効率良く取得するかが課題となる。我々は自動分注機及びプレートリーダーを利用することで,試料調整と吸収波長の測定を効率良く行うことを考えた。プレートリーダーはマイクロウェルプレート中の試料の吸光度や蛍光スペクトルなどを自動で計測する装置である。
自動分注機での作業をFig. 2 に示す。試料液調整と,96ウェルガラスプレートへのキャスティングを全て自動で行った。吸収スペクトル測定の際は吸光度が低すぎず,かつ飽和しない程度に濃度を選択する必要がある。そのため,試料調整の際,一度の測定で適切な吸光度が得られるように1化合物につき3つの異なる濃度調整を行った。次いでそのウェルプレートをプレートリーダーにセットし(Fig. 3),96サンプルの吸収スペクトルを測定した。

以上の操作を行うことで,約800種の有機化合物の吸収スペクトルを取得し,最も長波長側のλmaxを機械学習の目的変数として使用した。一般的な分光光度計を用いた手作業による測定時間と比較すると,作業効率を約5倍に向上させることができた。
3 説明変数の生成
3. 1 構造の記述子と溶媒の極性パラメーターの生成
機械学習を行う前に,各構造の特徴を数値として記述した変数を用意する必要がある。本取り組みでは中性の有機化合物を対象にし,SMILES記法によってalvaDesc 4)で構造の記述子を生成して,その記述子を説明変数として使用した(Table 1)。
また,分光吸収スペクトル測定では溶媒の極性によってλmaxがシフトすることが知られている。この波長シフトの挙動を考慮するために,Rohrschneiderの極性パラメーター5)を説明変数に追加した(Table 1)。
Table 1 How to prepare the explanatory variable and the number of them before/after the dimensionality reduction.

3. 2 DFT/TDDFT計算による吸収波長の算出
各有機化合物の電子状態計算はGaussian16 6)を用いて,B3LYP汎関数と6-31G**基底関数の計算レベルで行った。DFT計算により基底状態における構造最適化を気相条件下で行い,次いでTDDFT計算を実行することで,各励起状態に対する吸収波長を算出した。得られた計算結果に対し,各励起状態への電子遷移における振動子強度を配慮しながら説明変数として使用する吸収波長を選定した(Table 1)。
4 予測モデルの作成と考察
4. 1 λmax予測モデルの作成
第三節で得られた有機化合物の化学構造の記述子,Rohrschneiderの極性パラメーター,TDDFT計算で求めた吸収波長を説明変数としてデータセットを作成し,中性の有機化合物を対象にしたλmaxの予測モデルの作成を試みた。
Scheme 1 に示したように,2151個のデータを,トレーニングデータとテストデータとして8:2 に分け,予測に必要な説明変数のみを効率的に抽出するためにLasso回帰等で各説明変数重要度を評価し,重要度が極めて低い説明変数を削除した。トレーニングデータを用いて説明変数を絞り込んだところ,構造の記述子に加えて,Rohrschneiderの極性パラメーターも重要な説明変数であり,溶液中におけるλmaxの予測では溶媒の極性に関するパラメーターが有効であると言える。さらに,TDDFT計算で算出した吸収波長は最重要因子として挙がっており,TDDFT計算結果を機械学習に組み込むことの有用性が示された。
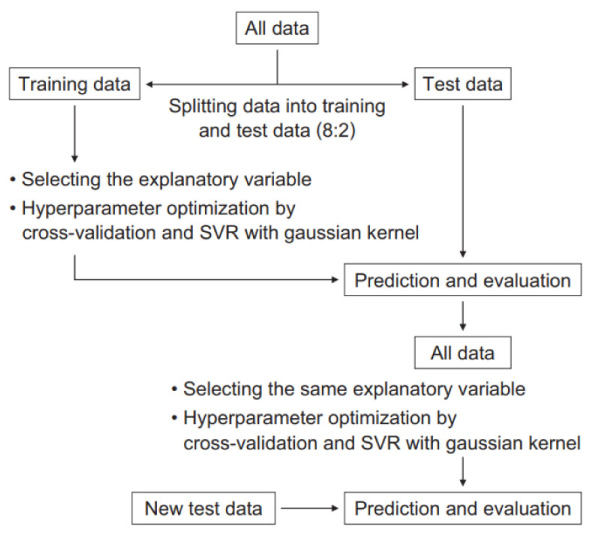
Scheme 1 Overview of the machine learning workflow.
説明変数の削減後に,ガウシアンカーネルを用いたSVR7)によって回帰モデルを作成した。その際,ハイパーパラメーターは10分割交差検証法で決定した。トレーニングデータによる回帰モデル(Fig. 4)ではR2値が0.98,RMSEが16.6 nmを示した(Table 2)。
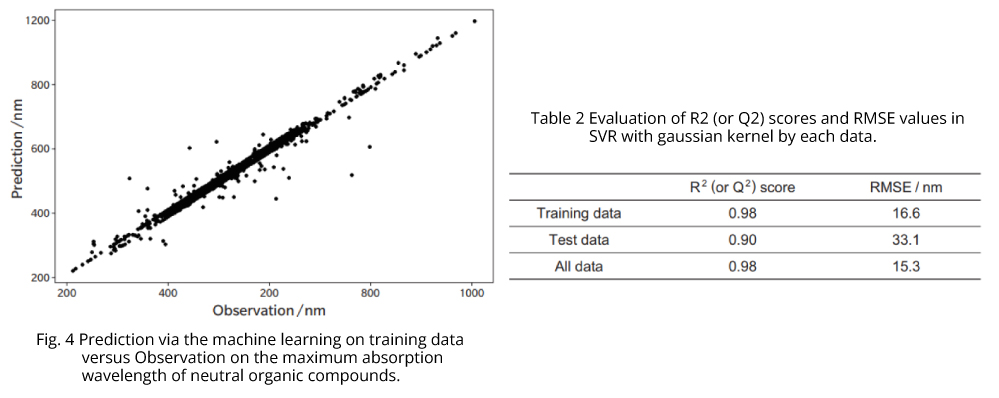
次に,回帰モデルを用いてテストデータを利用して検証したところ,以下の定義式(1)からQ2値が0.90,RMSEが33.1 nmであった(Table 2)。
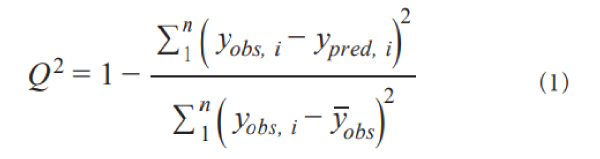
Fig. 5 から短波長側の予測精度が低いものがあるが,Q2値も高いことから,予測モデルは過学習をしておらず,汎化性能が高いと考えられた。
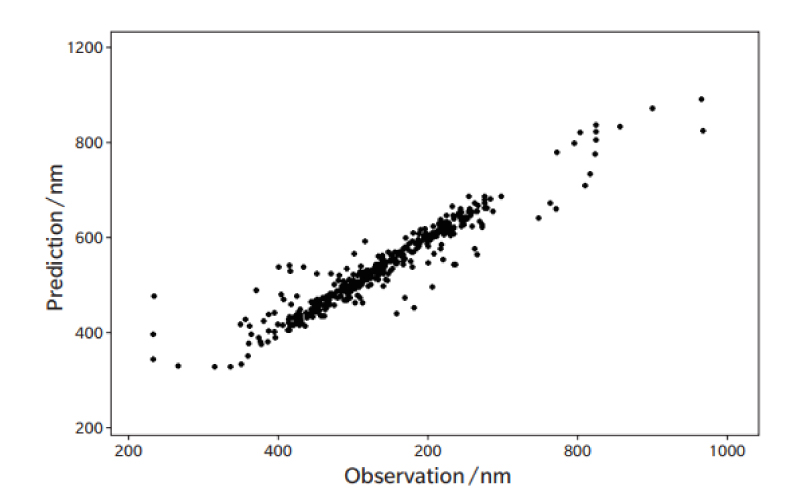
Fig. 5 Prediction via the machine learning on test data versus Observation on the maximum absorption wavelength of neutral organic compounds.
上記の結果から,説明変数の削減およびSVRによる予測モデルの作成方法には大きな問題がないことが分かった。そこで,特に重要度が高い説明変数を使用し,全データを用いたSVRによる予測モデルの作成を行った(Fig. 6)。その結果,R2値が0.98,RMSEが15.3 nmを示し(Table 2),予測精度がより高いことが分かった。
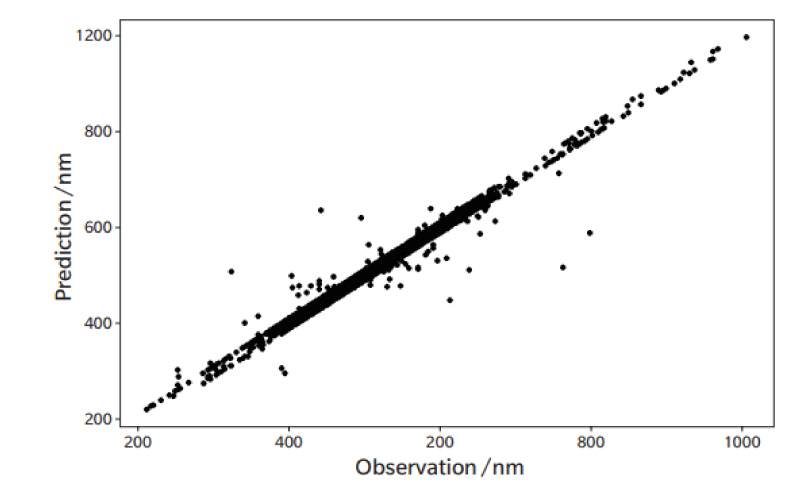
Fig. 6 Prediction via the machine learning on all data versus Observation on the maximum absorption wavelength of neutral organic compounds.
4. 2 予測モデルの予測精度と適用範囲に関する考察
4. 1で作成した予測モデルの予測精度を考察するために,新たに中性の有機化合物の実験データから48個のテストデータを用意し,本予測モデルを適用して得られたλmaxの予測値とその実験値を比較した。比較した結果,RMSEが39.7 nmと大きい値を示すことが分かった。これはテストデータにモデルの適用範囲外のデータが混在していることが原因と考えられる。
DFT/TDDFT計算とは異なり,機械学習では適用範囲の可視化を行うことで予測の信頼性を評価できる。この適用範囲はデータ密度と関係があり,データ密度が高いとモデルの適用範囲内であることを示す。そこで,k近傍法8)によりトレーニングデータの各データ間の距離を算出することでデータ密度を推定し,予測結果のRMSEに配慮しながらモデルの適用範囲を評価した。モデルの適用範囲を評価した結果,適用範囲内にあたるテストデータ数は12個と少ないものの,その適用範囲内のデータでの予測結果ではRMSEが8.4 nmを示し,予測精度の高いモデルを作成することができた。
以上から,本予測モデルは,膨大な有機化合物の候補から所望のλmaxを有する有機化合物候補を選定する方法として利用できる。また,今後は同様な方法によって実験及び計算データを増やすことで,予測モデルを改良することができ,モデルの適用範囲を広げることに繋がると期待できる。
5 結び
本稿では,DFT/TDDFT計算とハイスループット実験を組み合わせて機械学習に活用することで,λmaxの高精度な予測モデル(RMSE<10 nm)が構築でき,分光光度計を用いた手作業に比べ約5倍の作業時間の効率化を示すことができた。
本稿で作成した予測モデルは製品開発に向けた有機化合物の選定に利用できるだけでなく,本予測モデルの作成方法を応用することで,多様なテーマへの横展開が可能であり,今後のMIを活用した材料開発に貢献していきたい。



