1 はじめに
1.1 背景
これまで機器の内部データを監視することにより、故障要因判定による保守時間の短縮化、さらには経時変化を監視し寿命・故障予測を行うことで予知保全を行う等、機器のダウンタイム削減の取り組みが行われてきている。近年では、機器側でより高分解能でリアルタイムにデータが取得できる機能の搭載と、ネットワーク機器・インフラの発展により、顧客価値の高いサービスが提供できる環境が整ってきており、またその必要性も増してきている。
デジタル印刷機器でも、予知保全による顧客価値の高いサービスの提供が求められている。提供するサービスの中には予知保全のための故障予測がある。近年データドリブン (機械学習) による正常/異常の予測が積極的に活用されているが、まれにでも高額部品の予測外れが発生することで、現場の使用頻度が大きく低下する事例も報告されている。使用頻度が下がる原因は判定・予測精度が上がらないことにある。下記にその理由を挙げる。
1.World Wideで4,000~6,000種あると言われる紙種への適用、顧客が期待する多種多様な画質レベルなど、顧客の使用条件の多様性
2.デジタル印刷システムは、画像描画や用紙搬送のメカニカル技術、それを制御するエレクトロニクス技術、画像処理技術、画像形成プロセス技術、材料技術など多くの要素技術が組み合わされており、各機能間の関連が複雑になっている
これらを解決する手段として、演繹的アプローチとしては機器内部の構造を定式化したモデルを設計し、目標値との偏差から判定・予測を行うことが望ましいが、上記理由により機器状態を定式化する事は非常に困難という課題がある。また帰納的アプローチとしては、データドリブン (機械学習) が利用されているが、機器の経時的な状態変化 (トレンドなど) を表現することが難しく、また判定に用いるデータを偏りなく収集する必要があるなど課題も多く、入力の変動に対して頑健な予測モデルを設計することは難しい。
そこで本テーマでは、発生メカニズムが複雑で全体像を明確にすることが容易でない事象を対象として機器の状態をモデル化し、機器内部の信号から現在の状態を推定し、使用条件の詳細を把握せずに判定・予測が行える技術コンセプトの確立を目指した。
2 提案技術
2.1 システム構成と概要
本テーマでは、この課題を解決するために、機器状態がマルコフ過程に従うことのみを仮定し、内部信号から機器状態を直接モデル化するとともに、運用時においても内部信号を入力として現在の状態を推定することで、使い方や状態トレンドに影響されずに状態判定が行える技術を構築した。
今回対象とするデジタル印刷機器の状態システムをFig. 1に示す。顧客が期待する出力を提供するための機能を分解すると、機能が明確で定式化出来るものと、複雑に機能が組み合わされて定式化が困難なものに分けられる。これらが複合的に混在して機器状態を構成している。そこで、これら機能の状態を抽象化した信号Uconditionを生成することで機器の状態を得る手段になることが期待される。本テーマでは、この信号Uconditionを用いて、状態の変化を統計的に捉え予測する検討を進めた。
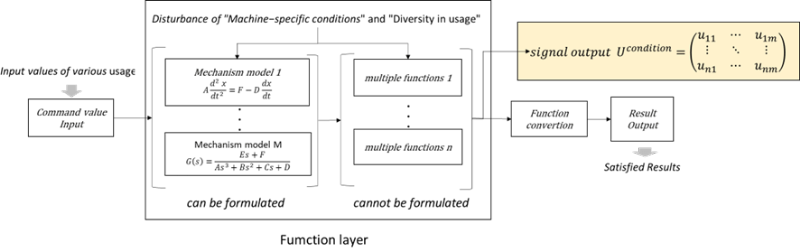
Fig. 1 System configuration for acquiring equipment status
2.2 状態推定手法
このような機器状態のモデル化に状態空間モデルを用いる方法を考えた。状態空間モデルとは、測定された変数を示す観測変数と、観測できない状態を表す状態変数に分解され、特に対象が定常性を保証できない非線形の時系列で高い推定効果が得られるモデルである。式(1), (2)に係数行列A, B, C, D, K、入力ベクトルut 、出力ベクトルyt、状態行列xt、誤差項 etの状態空間モデルの一般構造式を示す。誤差項はN(0, σ2)の白色ノイズを想定する。
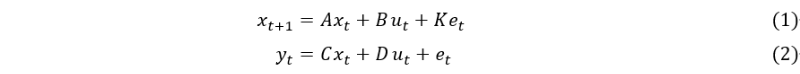
一般的な状態空間モデルの使い方として、時点の将来を逐次予測する手法 (点推定) がとられているが、機器の状態を測るとき、短期的なセンサー信号の状態のみを捉えると、周期の短い変動、いわゆるノイズの影響を受け、正確な状態検知することはできない。そこで、本テーマでは、機器状態を区間に分け、区間ごとに判定・予知を行う (区間推定) ことを考えた (Fig. 2)。
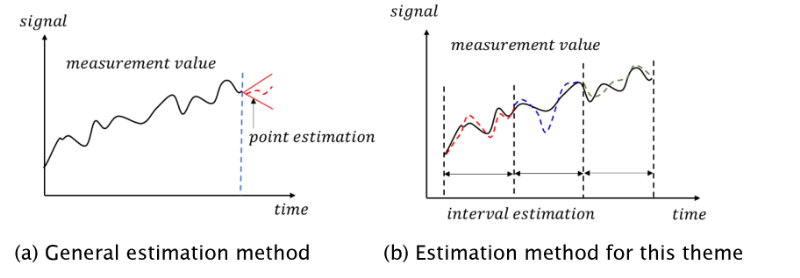
Fig. 2 Estimation method using state space model
Fig. 3に用紙搬送ユニットの構成を示す。印刷が開始されると、右端の給紙トレイから給紙された用紙が転写ローラー、定着ローラー等を経て搬送される。印刷が片面のみであれば用紙はそのまま図左端方向へ排出されるが、両面印刷の場合は左下へ搬送され、裏面印刷のためにスイッチバックを行い用紙の搬送方向を反転して上部に再給紙を行い、再度転写ローラー、定着ローラーを経て裏面へ印刷・搬送され、図左端より排出される。このような搬送動作を制御するために、用紙の搬送経路上には多くの搬送ローラー対と、用紙の先端・後端を検出するセンサーが設けられている。
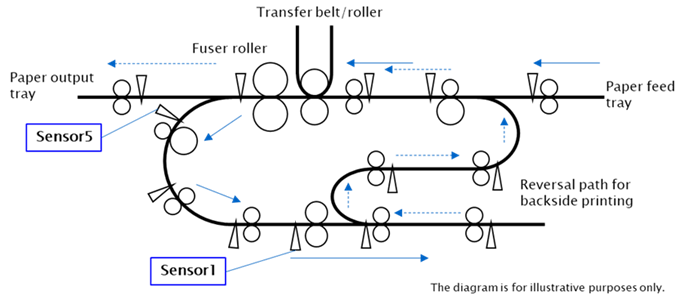
Fig. 3 Configuration example of paper transport unit
Fig. 4に状態空間モデルの同定に必要な具体的な入出力信号を示す。この例では用紙が通過する経路に設置するセンサー数を6個{s1, s2, s3, s4, s5, s6}とし、入力ベクトルに上流に位置するセンサーs5の出力信号(通過時間) ulearn s5 1:n={ulearn s5 1, ulearn s5 2, …, ulearn s5 n }、 出力ベクトルに下流に位置するセンサーs1の出力信号(通過時間) ulearn s1 1:n={ulearn s1 1, ulearn s1 2, …, ulearn s1 n }を状態空間モデルに代入し同定計算に用いた。ここでは用紙の繰返し測定枚数を表す。
この系の場合、センサーs5を入力に用いることで、状態の予測に関係のないトレンド成分を除去することが出来る。
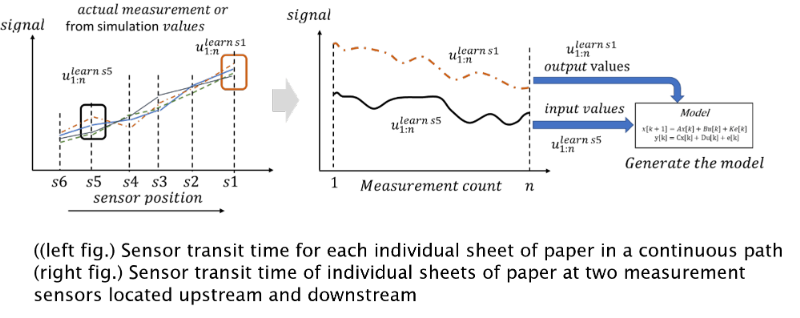
Fig. 4 Model learning of equipment state
式(3), (4)に同定に用いる状態空間モデルの構造方程式を示す。機器の状態によっては長時間の時系列データが得られないため、同定には少ないデータ量から分解能の高い情報が得られる部分空間同定法[1]を用いた。
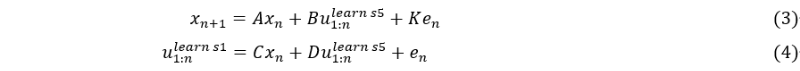
次に正常、異常を判定する推定値の導出方法についてFig. 5に示す。同定された係数行列を用いて、実機から繰返し区間 [1:n] の実測値データ uobs s5 1:n={uobs s5 1, uobs s5 2, …, uobs s5 n } を収集する。入力ベクトルに上流に位置するセンサーs5の出力信号を代入し状態空間モデル式を解くと下流に位置するセンサーs1の出力信号の推定値y^ s11:n={y^ s11, y^ s12, …, y^ s1n} が得られる。状態式を式(5), (6)に示す。
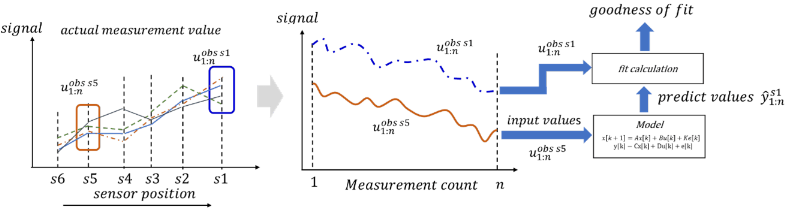
Fig. 5 Method of determining equipment state
式(5)の誤差項を式(6)で消去し式(7), (8)を得る。推定式のため誤差項は期待値の0とする。
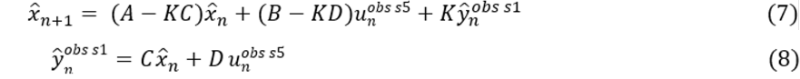
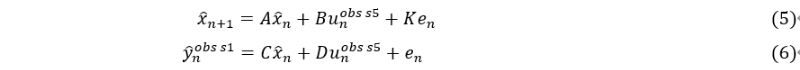
センサーs1の実測値 uobs s1 1:n{uobs s1 1, uobs s1 2, …, uobs s1 n } と、状態空間モデル推定値 y^ s11:n{y^ s11, y^ s12, …, y^ s1n} との区間相関を取ることで、正常状態との適合率(fit)を算出する。適合率計算式[2]を式(9)に示す。このfitは、時系列データの全てにおいて予測値と実測値が一致しないと100%とならないため、実測値に繰り返しバラツキや用紙サイズバラツキ等の誤差を含む以上100%にはならない。また、誤差が大きいと負の値をとることに注意する。
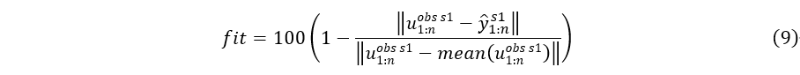
同様に、異常状態のセンサーの実測値データから、異常状態のモデルを生成し、異常状態との適合率も算出することができる。
3 実験と考察
3.1 実験の概要と条件
実験対象として、商業用デジタル印刷システム (製品名:Accurio Press C7100) の用紙搬送ユニットを使用し、異常状態として用紙搬送ジャム (紙詰まり) が発生する状態のモデル化と状態判定を実施した。
このような用紙搬送系において発生する異常現象として用紙搬送ジャムがあり、用紙搬送制御上、許容される時間内にセンサーによって用紙の先端・後端が検出されなかった場合、紙詰まりが発生したと判定され用紙搬送ジャムとなる。このような現象が発生する要因としては、用紙搬送ローラーのスリップによる搬送遅れ、搬送ローラーの駆動負荷が増加して発生するモーターの脱調 (回転不良) による搬送遅れ等が挙げられる。ローラーのスリップ、ローラーの駆動負荷増加は経時的な劣化で発生に至ることもあるが、前述のように市場での使われ方は多種多様であり、特に紙種は1000種を超えるため、用紙によってはスリップや駆動負荷増加が起こりやすいものもある。搬送ローラーのスリップと駆動負荷増加による用紙搬送遅れが発生し、用紙搬送ジャムと判定されるまでには経時的に徐々に遅れが増加していくように思われるが、実際はローラーの搬送グリップ限界を超えた状態、あるいはモーターが同期回転を保持できる許容負荷を超えた状態で突然破綻に至るため、破綻に至る直前の微少な搬送タイミングの変化を捉える必要がある。この微少な変化は通常の搬送バラツキの要因である各搬送ローラー径のバラツキによる速度誤差、ローラーのスリップ率のバラツキによる速度誤差、紙のバタつきやカール (丸まり) による先端・後端の搬送タイミングずれに埋もれてしまい、明確に閾値で判定することは困難である。このような系は前述した通り、短期的なセンサー信号の状態のみでは周期の短い変動(ノイズ)の影響を受け正確な異常値を検知することはできず、状態がトレンドで徐々に異常状態に近づいていくケースであり、前項2-2で提示した方法に沿って系の同定と異常状態の判定を検証した。
3.2 状態のモデリング
用紙搬送ユニットのセンサーの中から、正常状態と用紙搬送ジャムが発生している異常状態で何らかの (理由は不問である) 変化が生じているセンサーを探索し、ある二つのセンサーにおいて用紙後端が抜けるタイミングに変化が出ていることが分かったため、これらのセンサーをFig. 4及びFig. 5におけるs5, s1として使用した。モデル化の概要をFig. 6に示す。Fig. 6におけるモデル化に際しては、状態判定結果を相互評価するため、用紙搬送ジャムが発生してない正常状態の機器と、用紙搬送ジャムが高頻度で発生している異常状態の2パターンの機器を用意した。センサーデータは、Fig. 6の上側の図のように用紙の有無に応じてHi/Loレベルが変化するデータであり、これを用紙の通紙周期に応じて繰り返す波形となる。正常状態の機器と異常状態の機器のそれぞれに対して連続で複数ページの印刷を実行し、入力ベクトルとして上流に位置するセンサーs5の出力信号u learn s51:n、出力ベクトルとして下流に位置するセンサーs1の出力信号u learn s11:nを収集し、式(3), (4)の状態空間モデルのシステム行列を同定し、正常状値モデルと異常状態モデルを設計した。
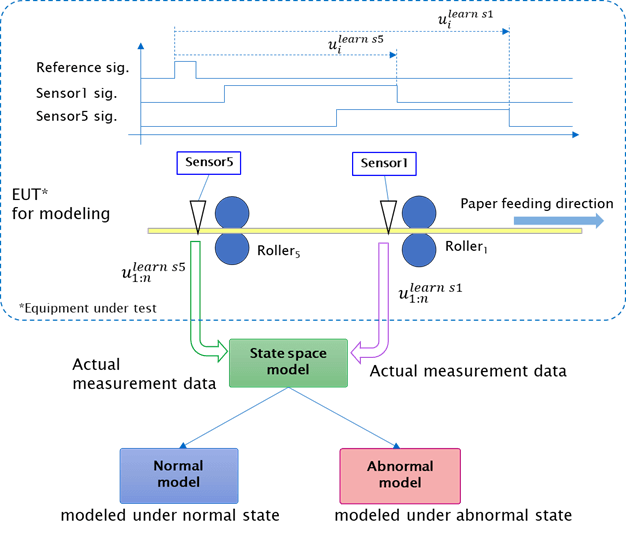
Fig. 6 Equipment state modeling
3.3 実機器を用いた適合率による機器状態判定
次に、同定したモデルを用いて実際に機器の状態判定を検証した。異常状態モデルと正常状態モデルのそれぞれに対し、同一の実測値を用いてモデル予測値算出と適合率計算を実施した。その構成をFig. 7に示す。
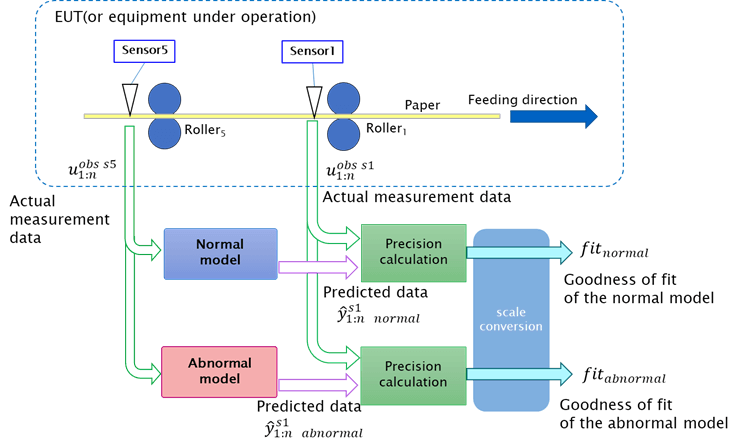
Fig. 7 Determination of equipment state
Fig. 7において、運用 (動作) している機器から得たセンサーs5のデータu obs s51:nを両モデルに入力しセンサーs1の予測値 y^ s11:n normal 及び y^ s11:n abnormal を得る。同時にセンサーs1の実測値 u obs s11:n も得られるため、それら予測値と実測値を一定量収集する毎に正常状態モデルの予測値 y^ s11:n normal とセンサーs1実測値 u obs s11:n の適合率、及び異常状態モデルの予測値 y^ s11:n abnormal とセンサーs1の実測値 u obs s11:n の適合率を算出する。得られた適合率から現在の機器の状態 (実測データ) がどちらのモデルに近いかを定量的に判定した数値として得られる。以上の計算を正常状態の機器と異常状態の機器に対して適用するため、組み合わせパターンはTable 1に示した通り、a)-d)の4パターンとなる。
Table 1 Verification conditions
3.4 分析と考察
a)-d)の4パターンにおけるセンサーs1実測値 u obs s11:n とモデルの予測値 y^ s11:n について、正常状態機器に適用したものをFig. 8に、異常状態機器に適用したものをFig. 9に示す。
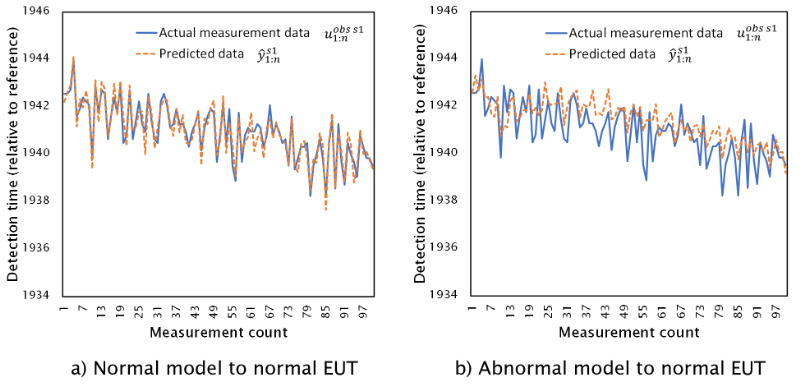
Fig. 8 Prediction results of normal and abnormal models on normal state equipment
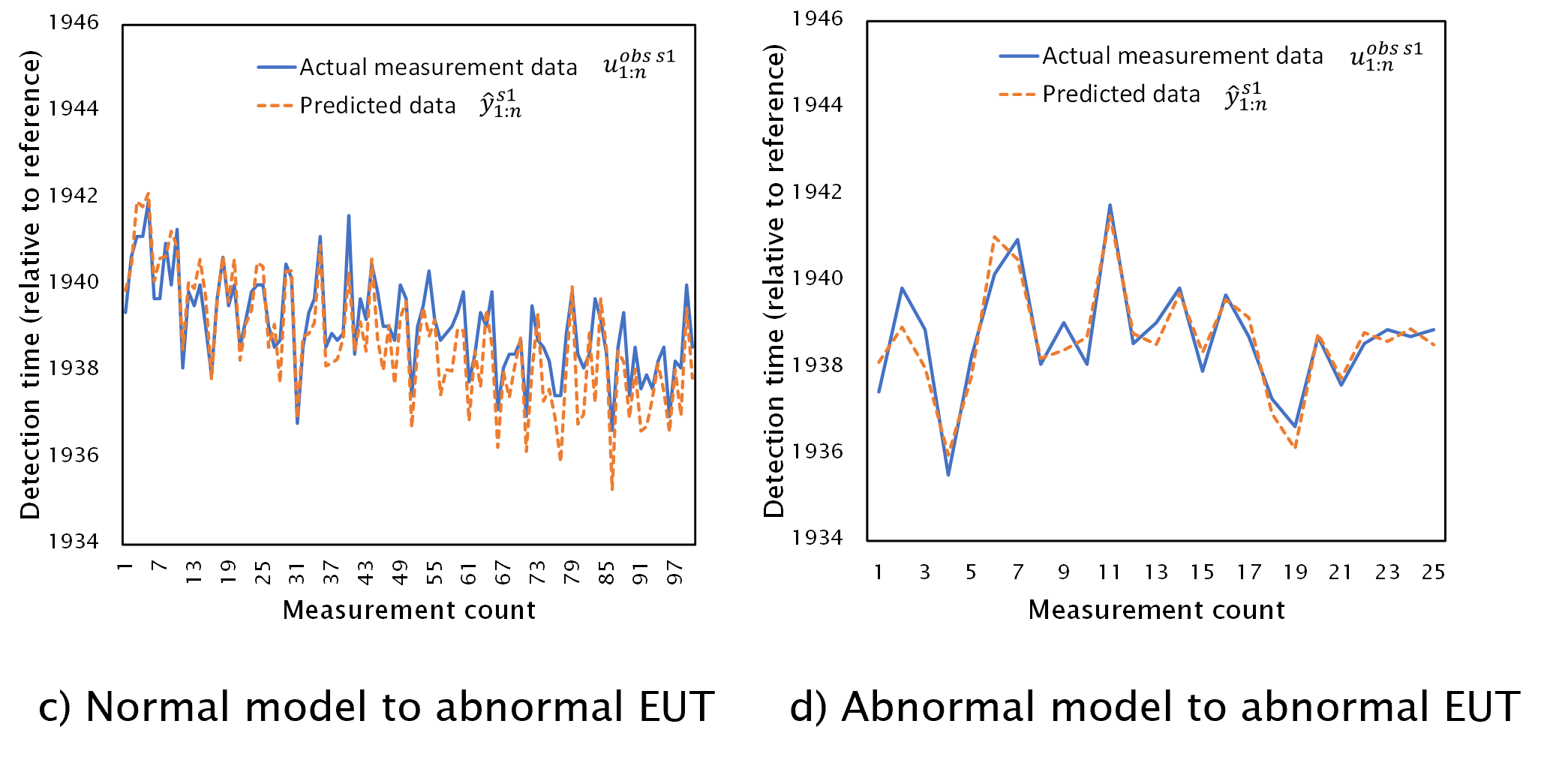
Fig. 9 Prediction results of normal and abnormal models on abnormal state equipment
また、a)-d)の適合率(fit)判定結果をTable 2にまとめた。
Table 2 Fit rate (fit) determination results

Table 2より、正常状態機器における実測値に対し、正常状態モデルの予測値適合率は69%、異常状態モデルの予測値適合率は21%となり、相対的に正常状態モデルの適合率が高いという結果が得られた。異常状態機器における実測値に対しては、正常状態モデルの予測値適合率は25%、異常状態モデルの予測値適合率は64%となり、相対的に異常状態モデルの適合率が高いという結果となった。これにより機器状態を定量的に判断するための指標が得られたと考える。
4 まとめ
本論文では、機器状態がマルコフ過程に従うことのみを仮定し、部分空間同定法を用いて内部信号から機器状態を直接モデル化するとともに、運用時においても内部信号を入力として現在の状態を推定することで、使い方や状態トレンドに影響されずに状態判定が行える手法を示した。状態判定には時系列データの予測値と実測値に対して適合率 (fit) を計算することで機器状態を定量的に判断するための指標が得られた。今後は実用に向けて、サービス現場での実情と指標を対応付ける、あるいは現場での運用を通じて指標に対するサービスアクションを定めていくといった運用での使いこなしによって市場適用できるようにしていく。



