1 はじめに
複合機や自動車などの大型の実製品に対しても開発期間やコスト削減を目的に設計の初期段階から EMC(Electromagnetic Compatibility)を考慮した設計,いわゆるEMC設計をコンピュータ上で実現し,試作回数を最少化することが求められている。三次元電磁界シミュレータによる電磁界解析では,実製品の構造を忠実に再現した実構造モデルに基づいてシミュレーションを行うことで,不要放射が予測可能である。計算時間に関しても計算機性能向上に伴い,実用可能な時間で計算できるようになっている。
しかし,電磁界解析に基づき不要放射の原因となりうる要素と算出結果の因果関係を理解することは依然として困難であり,不要放射の原因究明には条件を変えた繰り返し計算が必要となる。そのため膨大な計算コストが必要となる。複合機や自動車のような金属筐体に通信ケーブルが張り巡らされた構造からの不要放射はコモンモードが支配的と考えられる。これは,ノーマルモード放射は信号伝送系の線路間隔を小さくすることで抑制が可能であり,不要放射への影響が小さいためである1)。一方,コモンモードはその経路により形成されるループ面積がノーマルモードより大きく放射量も大きい。線路の平衡度の変化で生じるコモンモードへのモード変換はコネクタ設計や筐体上のケーブルの引き回し次第で増減する。
そのため,コモンモード励振源やその原因となる構造を設計の初期段階で特定し,コモンモード放射を抑制するケーブルや筐体構造およびケーブル配置の決定することが,不要放射抑制にとって重要である。なぜなら,設計の最終段階における配線経路や送受信基板位置などの変更は,設計全体への影響が大きく困難となるためである。よって,EMC設計実現にはコモンモード発生原因であるモード変換を取り扱えるモデルが必要である。
モード変換によって生じるコモンモード電流やコモンモード放射を予測する手法として,コモンモードアンテナモデル2) 3) 4)やモード等価回路モデル6)がある。これらのモデルは伝送線路の平衡度に着目し,平衡度が変化する場所で,その変化量に応じて生じるモード変換を表現しており,平衡度不整合モデルと呼ばれる。平衡度不整合モデルを用いることでモード変換によって生じるコモンモード電流やコモンモード放射の評価が可能である。
先行研究ではコモンモードアンテナモデルは平衡度が異なる伝送線路を有するプリント回路基板(PCB)2) 3) 4)やコネクタ接続されたPCB5)のような単純な構造を対象としており,モード等価回路モデルもモデルパラメータが線路に沿った方向にのみ変化する構造を対象としていた6) 7)。本論文では実製品の例として複合機を模擬した被試験機器(Equipment Under Test: EUT)を対象に平衡度不整合モデルと三次元実構造モデルとの結果を比較し,放射量が概ね一致すること,つまりEUTからの不要放射はコモンモード放射が支配的であることを示し,さらに平衡度不整合モデルを用いることで支配的な放射の元となるコモンモード励振源を特定可能であることを示す。不要放射の評価は複合機の実際の不要放射試験に則って,Fig. 1 のように放射中心から半径10 mの円筒面上の電界の水平偏波と垂直偏波の最大放射スペクトルを評価する8)。
本論文ではまず,2で平衡度不整合モデルを用いた不要放射予測法について示す。次に,3で本論文において評価を行うEUTのモデル構造について示す。最後に,4で実構造モデルの三次元電磁界シミュレーションとの比較結果と平衡度不整合モデルを用いることで支配的な放射の元となるコモンモード励振源を特定可能であることを示す。
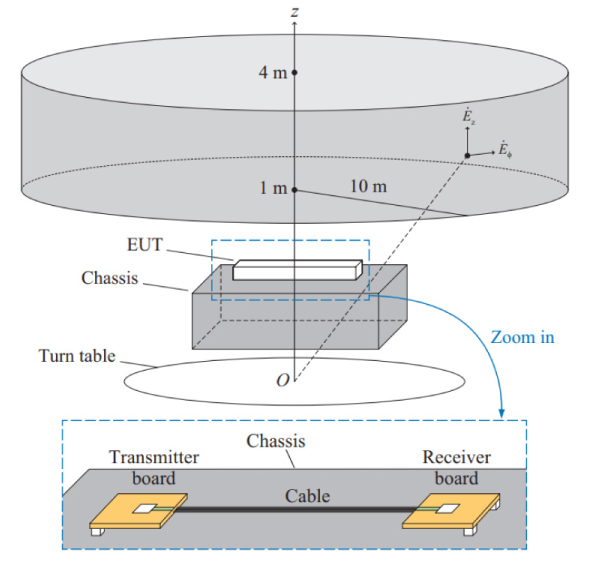
Fig. 1 Evaluation system for radiation.
2 平衡度不整合モデルを用いたEMC設計
2. 1 平衡度不整合モデル
本論文で取り扱う平衡度不整合モデルに関してFig. 1のEUTを例に説明する。
2. 1. 1 平衡度不整合モデルの利点
複合機や自動車には金属筐体近くに送受信基板をケーブルで接続した複数の通信系を内包しているため,EMC規格を満たさなかった場合に設計の最終段階でそのような通信系の基板配置や配線ケーブルの引き回しを変更することは設計スケジュールへの影響が大きく現実的ではないため,対症療法的なノイズ対策に頼りがちである。そのため,ケーブル接続された通信系は設計の初期段階で不要放射を抑制する配置にするのが肝要である。また,Fig. 1 のように筐体近くに配置された通信系は線路の2導体に加えて金属筐体が近接するため,2導体線路と筐体をシステムグラウンドとして扱った3導体で構成される。この場合,3導体伝送系ではノーマルモードとコモンモードの二つの直交モードが存在し,このコモンモードが不要放射発生の主要因となる。そのため,設計の初期段階からコモンモード放射を生じさせない配慮が必要である。
平衡度不整合モデルのコモンモードアンテナモデルおよびモード等価回路モデルは線形モデルである。そのため,EUTが複雑化しモード変換が複数箇所で生じる場合であっても,各モード変換によって発生するコモンモード電流やコモンモード放射の線形和より合成電流や合成電界を得られる。言い換えると,複数の励振源を1つずつ励振することで支配的な放射の元となる励振源を特定可能である。その結果,設計の初期段階で平衡度不整合モデルを用い,コモンモード放射への寄与が大きいコモンモード励振源に対して対策を行うことでコモンモード放射を抑制した配置を実現できる。
2. 1. 2 モード等価回路モデル6) 7)
Fig. 1 のEUTのモード等価回路はFig. 2 で表される。伝送系に生じる電磁界をTEMモードで近似できる範囲では,実電圧と実電流をモード分解することにより,3導体伝送系はノーマルモードとコモンモードの伝送線路に分けて表される9) 10)。
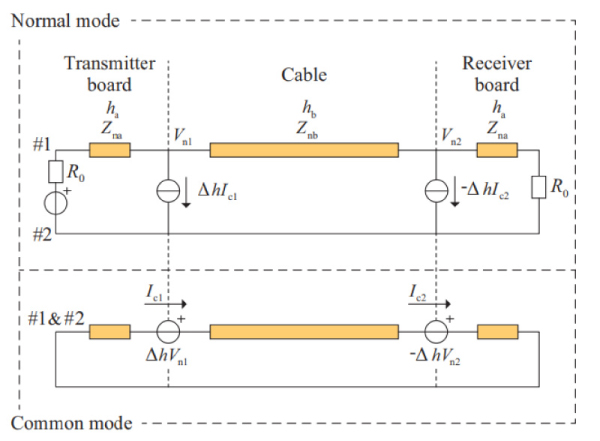
Fig. 2 Modal equivalent circuit model of signal trans-mission system shown in Fig. 1, where Δh=hb–ha.
Fig. 1 の送受信基板とケーブルの平衡度を表す電流配分率3)をそれぞれ,ha,hbとし,これらは異なる値をもつとする。つまりFig. 1 のEUTは異なる電流配分率をもつ線路が接続されているため,その境界で電流配分率の差Δhが生じる。Δh=hb−haとすると,送信基板とケーブル間にΔh,ケーブルと受信基板間に−Δhの電流配分率の変化が生じ,モード変換は電流配分率が変化するその境界で生じる。そのため,Δhとその境界におけるノーマルモード電圧Vnを用いて表されるノーマルからコモンへのモード変換を意味するコモンモード励振源ΔhVnがコモンモード等価回路に直列に挿入される。さらに,Δhとその境界におけるコモンモード電流Icを用いて表されるコモンからノーマルへのモード変換を意味するノーマルモード励振源ΔhIcがノーマルモード等価回路に並列に挿入される。このようにしてモデリングされたモード等価回路モデルを用いることで各コモンモード励振源に起因するコモンモード電流Ic1,Ic2を求めることができる。
2. 1. 3 コモンモードアンテナモデル 2) 3)
コモンモードアンテナモデルはFig. 2 の等価回路におけるコモンモード等価回路部分のみを再現した三次元モデルである。Fig. 1 のコモンモードアンテナモデルはFig. 3のようになる。
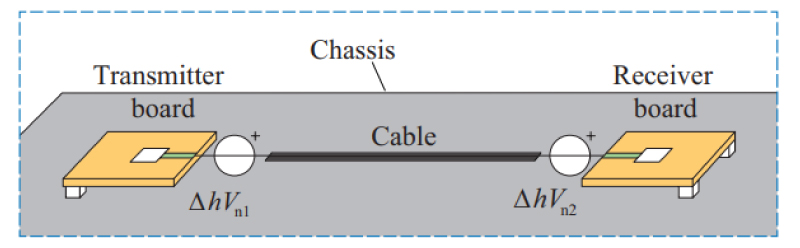
Fig. 3 Common-mode antenna model of signal trans-mission system shown in Fig. 1.
コモンモード励振源を1つずつ配置したモデルを用いることでそれぞれのコモンモード励振源に起因して生じるコモンモード放射Ec1,Ec2を求めることができる。また,アンテナエレメントとなるケーブル部の2導体はコモンモードにおいては同電位であるため,コモンモードアンテナモデルでは両導体を1つの導体としてモデル化する。マイクロストリップ線路のように信号線が帰路面より十分狭い場合,信号線のコモンモード放射への影響は帰路面より十分小さいため,コモンモードアンテナモデルではマイクロストリップ線路部の形状をその帰路面形状で与える。このようにコモンモードアンテナモデルはアンテナエレメントに相当する導体部の微細な構造を省略し,電磁界シミュレーションにおける被解析構造を簡略化できる。
コモンモードアンテナモデルの電磁界シミュレーションにおいても実際の不要放射試験に則って,最大放射スペクトルを計算する。そのため,コモンモードアンテナモデルによるコモンモード放射スペクトルは以下の手順で算出した。
(1)Fig. 3 の各モデルでシミュレーションを行い,各地点においてEc1とEc2を求める。
(2)Ec1とEc2の線形和を水平偏波と垂直偏波ともに算出し,その結果から全地点の最大値をとることで,放射スペクトルEcを決定する。
2. 2 平衡度不整合モデルを用いた放射予測
モード等価回路モデルとコモンモードアンテナモデルの両者の平衡度不整合モデルを Fig. 4 で示すフローチャートにより連成して解くことで,Fig. 1 に示すEUTからの放射予測が可能である。まず,①ノイズ発生源となりうる場所を抽出する。次に②ノイズ発生源に対して,モード等価回路モデルでコモンモード電流Ic’とノーマルモード電圧Vnを求める。③コモンモードアンテナモデルに①で得られたVnを与えコモンモード電流Ic’’およびコモンモード放射Ecを求め,④モード等価回路モデルで求めたIc’とコモンモードアンテナモデルで求めたIc’’を比較し一致した場合は,Ecを出力し放射予測を終了する。Ic’とIc’’が一致しない場合はモード等価回路モデルで与えるコモンモード放射に相当する損失を変更して②からやり直す。
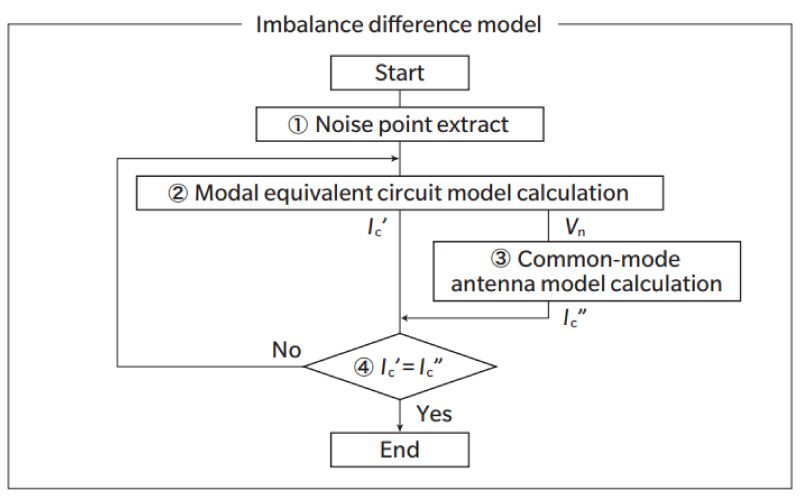
Fig. 4 EMI simulation flow chart using imbalance di erence model.
次節以降で,実際に実構造の例として複合機を模擬した構造を対象に,平衡度不整合モデルを用いることで支配的な放射の元となるコモンモード励振源とその原因の特定が可能であることを示す。
3 評価モデル構造
本論文において評価するEUTの構造を示す。EUTの構造をFig. 5 に示す。EUTは複合機を模擬した構造となっており,筐体上面に設置されている送信基板と側面に設置されている受信基板がフレキシブルフラットケーブル(Flexible Flat Cable: FFC)で接続されている。床面の原点Oからz軸方向に100 mmの位置に評価系の底面の中心を設置しており,床面とEUTの電気的な接続はない。
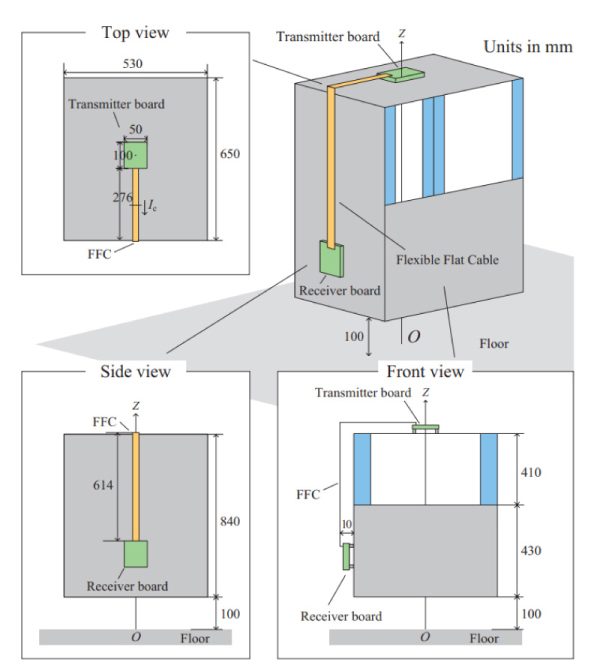
Fig. 5 Real structure model imitated multifunction Peripherals.
Fig. 6 は筐体を含むFFC部の断面構造である。FFCは内部に20本の導体を有しており,各導体は0.18mm間隔で配置されている。FFCと筐体の距離は10 mmである。
送受信基板は互いに同様の配線パターン構造をしており,例としてFig. 7 に送信基板の拡大図を示す。FFCの20本ある導体のうち中央の1本を信号線とし,基板上のマイクロストリップ線路の信号導体と接続している。その両隣のFFC導体は帰路線となるよう送受信基板のグラウンドに接続している。残りの17本の導体は送受信基板において50 Ωで終端している。電流配分率は近接導体と各線路間の容量から求まる6)ため,FFCの電流配分率は中央の信号線と筐体間の容量およびその両隣の線路と筐体間の容量を求めることで算出した。
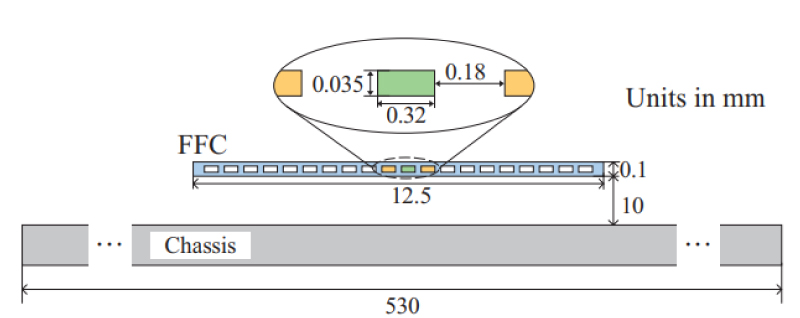
Fig. 6 Cross-section view of FFC.
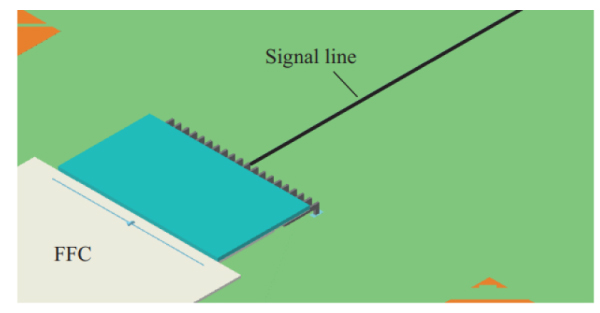
Fig. 7 Expanded view of transmitter board used for real structure model
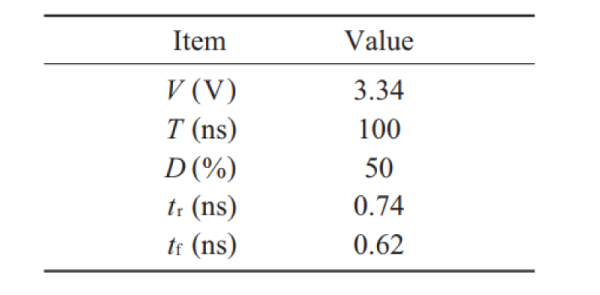
実構造モデルの解析には三次元電磁界シミュレータ(Fujitsu Poynting for Microwave)を用いた。実構造モデルの送信基板に実装した信号源から送信した信号のパラメータをTable 1 に示す。送信信号には,パルス振幅Vが 3.34 V, 周 期 T が 100 ns の 台 形 パ ル ス を 用 い た。デューティ比Dは50 %,立ち上がり時間trおよび立ち上がり時間tfはそれぞれ0.74 nsおよび0.62 nsである。コモンモードアンテナモデルとモード等価回路による解析では,まず信号源を単位電圧源として計算し,得られた結果をTable 1 で規定する台形波のスペクトルの包絡線で補正する。
Table 1 Parameters of trapezoidal pulse used as transmission signal.
三次元電磁界シミュレーションで得られるIcは放射による損失の影響を含んでいる。回路シミュレーションでもこの放射による損失を表現するため,等価回路モデルと実構造モデルで計算されたコモンモード電流Icとノーマルモード電圧Vnが同等となるような線路損失を与えた。
送受信基板とFFCの電流配分率が異なるため,送受信基板とFFCの接続部でモード変換が生じる。次節で送信基板とFFC間で生じるモード変換に起因するコモンモード電流 Ic1およびコモンモード放射Ec1とFFCと受信基板間で生じるモード変換に起因するコモンモード電流Ic2およびコモンモード放射Ec2をそれぞれ比較し,支配的なコモンモード励振源の判定が可能かを確認する。
4 複合機を模擬した構造を用いた評価
4. 1 モード等価回路を用いた評価
まず,Fig. 4 内の②モード等価回路による評価を行う。三次元電磁界シミュレーションにおいてコモンモード電流はループ形状の電流モニタにより測定した。電流モニタは筐体上面に沿って配置されているFFCの中央付近がコネクタやスリットから距離があり磁界分布が比較的安定していると考え,その位置に設置した。Fig. 5 の評価対象の上面図中にIcで示している。モード等価回路を用いた回路解析には市販の回路シミュレータ(Cadence AWR Microwave Office)を用いた。Fig. 1 とFig. 5 の信号伝送系の構造はどちらも送受信基板とケーブルで構成されているため,等価回路モデル構造は同様である。そのため,回路解析にはFig. 2 のモード等価回路モデルを使用した。Table 2 は回路シミュレーションに用いた諸パラメータである。特性インピーダンス,実効比誘電率,電流配分率は二次元電磁界シミュレータ(ANSYS 2D Extractor)を用いてそれぞれの線路の断面構造から算出した。
Table 2 Parameters used for circuit simulation.
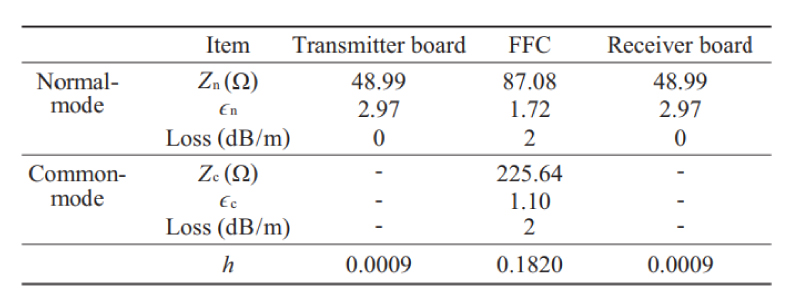
実構造モデルの三次元電磁界シミュレーションとモード等価回路を用いた回路シミュレーションにより算出したIcとVnの比較をFig. 8 に示す。Fig. 8 (a) の実線から高周波では誤差が増加するが,0.1 GHz ~ 0.5 GHzで生じる伝送系全体を共振器長としたコモンモード共振を再現できており,ピーク強度も概ね一致している。490 MHzでピーク強度に差があるように見えるのは,実構造モデルにおいて共振ピークがずれているためである。このことから,EUTで生じるモード変換の影響をモード等価回路で再現できていることが分かる。
次にFig. 8 (a) の破線からIc1とIc2を共振周波数において比較すると全周波数帯域にてIc1が支配的であることが分かる。コモンモードを発生させるコモンモード励振源はΔhVnで表されるので,Fig. 8 (b) の結果から線路損失の影響によってFFCと受信基板間のノーマルモード電圧Vn2が送信基板とFFC間のノーマルモード電圧Vn1より小さいため,Ic1が支配的となっていると考えられる。
以上より,モード等価回路によりIcを解析することで支配的なコモンモード励振源の推定が可能であり,また線路の平衡度や損失などから原因特定も可能である。
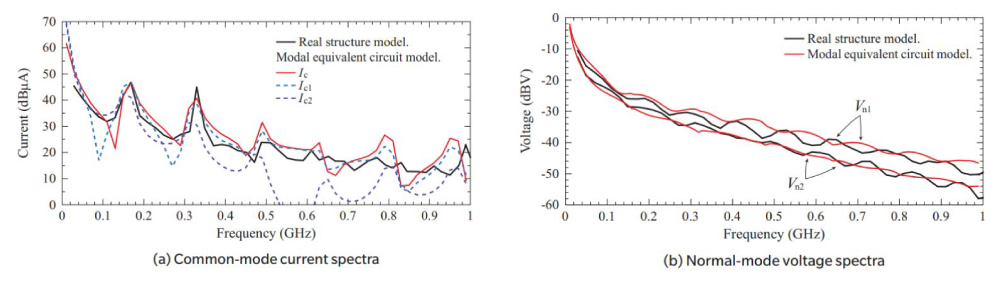
Fig. 8 Comparison of common-mode current and normal-mode voltage between of real structure model and modal equivalent circuit model.
4. 2 コモンモードアンテナモデルを用いた評価
次にFig. 4 内の③に示すようにコモンモードアンテナモデルによる評価を行う。放射解析は原点Oを中心とした半径10 mの円筒面上の高さを1 mから4 mまで0.5 m間隔で合計7箇所でい,各高さにおいて円周方向に5 deg間隔で合計72箇所,計504点における解析結果から各周波数における最大放射スペクトルを求めた。コモンモードアンテナモデルは三次元電磁界シミュレータ(ANSYS HFSS)を用いて電磁界シミュレーションを行った。
Fig. 5 のコモンモードアンテナモデルは 2. 1. 3で示したモデリング方法により,Fig. 9 のようになる。送受信基板とFFCの電流配分率は異なるため,送受信基板とFFCの接続間にコモンモード励振源が挿入される。コモンモードアンテナモデルのアンテナエレメントとなる導体部のうち,送受信基板の形状は帰路面形状とした。FFCで伝送線路として使用している導体はFFC中央にある3本のみだが,線路近辺にある導体は電磁界分布に影響があると考え,FFC部の形状は絶縁体を含むケーブル外形と同等の形状とした。
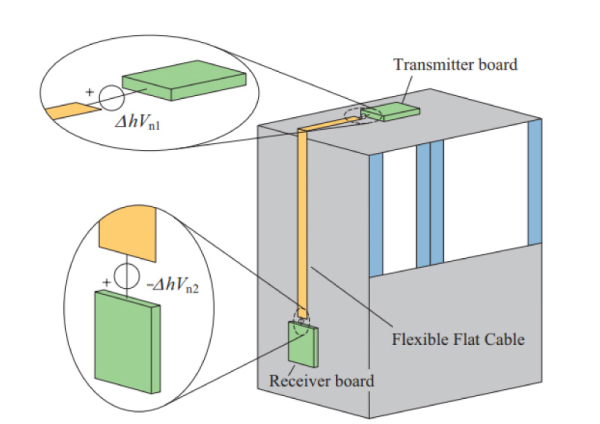
Fig. 9 Common-mode antenna model of EUT in Fig. 5.
実構造モデルとコモンモードアンテナモデルの比較をFig. 10 に示す。(a)と(b)はそれぞれ水平偏波と垂直偏波のスペクトルを示している。Fig. 10 の実線の結果からコモンモードアンテナモデルにおいても0.1 GHz–0.5 GHzでは伝送系全体を共振器長としたλ/2,λ,3λ/2,…のコモンモード共振のピーク周波数およびレベルが実構造モデルと一致している。このことから,複合機のように金属筐体と送受信基板をケーブルで接続された通信系で構成される構造で発生する不要放射はコモンモード放射が支配的であることが分かる。
次にFig. 10 の破線の結果からEc1とEc2では全周波数帯域においてEc1が支配的であることが分かる。これはモード等価回路の結果と同様に線路損失の影響によってVn2がVn1より小さいため,Ec1が支配的となっていると考えられる。
以上より,コモンモードアンテナモデルで評価することでコモンモード放射の元となる支配的なコモンモード励振源の特定が可能である。
Fig. 10 Comparison of radiation from EUT
5 まとめ
本論文では,平衡度の変化によって生じるモード変換を再現した平衡度不整合モデルを用いることで支配的なコモンモード励振源の特定が可能であることを示した。複合機を模擬した構造をEUTとして,実構造モデルの三次元電磁界シミュレーション結果と比較し,放射量が概ね一致したことからEUTから生じる不要放射はコモンモード放射が支配的であることを確認した。さらに,各コモンモード励振源からのコモンモード電流やコモンモード放射の結果から不要放射の支配的な励振源を特定できることを示した。
今後は平衡度不整合モデルにより特定したコモンモード励振源への対策によりコモンモード放射を抑制した設計が可能であるかを検討するため,筐体構造やFFCの配線位置を変更したEUTに対しても同様に支配的なコモンモード励振源が特定可能かの検討を行いたいと考えている。



